Porsche's BEVs Supply Chain Optimization

Business Case Overview

News: Porsche’s EV sales target

According to the news article, Porsche is facing difficulties in producing its battery-electric vehicles (BEVs) due to supply chain issues. These problems include sourcing critical parts like high-voltage heaters, which are essential for BEV production. Despite these challenges, Porsche has kept its goal of having BEVs account for 12-14% of its total sales. The company reported increased profits and sales in the first half of the year but is struggling to meet demand because of unpredictable supply chain disruptions. Porsche’s ability to meet its BEV targets depends on improving its supply chain in the second half of the year.

They need to make decisions about:

• Which suppliers to use to source these critical parts.
• How much of each part to order from each supplier.
• How to allocate parts efficiently to meet production needs while minimizing costs.

---

Objective: Minimizing Total Costs

\[\text{Minimize} \quad \sum_{i,j} c_{ij} x_{ij} + \sum_i p_i y_i\]

Let’s break down our objective function and understand what each terms mean:

• Porsche wants to minimize the total costs associated with its supply chain.
• $\sum_{i,j} c_{ij} x_{ij}$ : represents the ordering and transportation costs. Here, $x_{ij}$ is how many parts we order from supplier $i$ and send to factory $j$, and $c_{ij}$ is the cost of ordering and transporting those parts.
• $\sum_{i} p_{i} y_{i}$ : represents the penalty costs for working with suppliers who might have delays or disruptions. Here, $p_{i}$ is the penalty cost associated with supplier $i$, and $y_{i}$ is a binary variable (0 or 1) that tells us whether we’re using supplier $i$ or not. For example, if $y_{i} = 1$, it means the supplier is selected, and we may incur penalties for delays.

Constraints:

1. $\sum_{i}x_{ij} \geq d_{j} \quad \forall j$
   • Porsche’s factories (indexed by $j$) need a certain number of parts to build cars. Here, $d_{j}$ is the demand for parts at factory $j$.
   • $\sum_{i}x_{ij}$ : represents the total number of parts sent to factory $j$ from all suppliers $i$.
   • $\sum_{i}x_{ij} \geq d_{j}$ ensures that each factory receives enough parts to meet their production needs. So, we must order at least as many parts as each factory requires.
2. $\sum_{j}x_{ij} \leq S_{i} \quad \forall i$
   • Each supplier $i$ can only produce a limited number of parts, which is represented by $S_{i}$, the capacity of supplier $i$
   • $\sum_{j}x_{ij}$ : represents the total number of parts ordered from supplier $i$ (to be delivered to all factories $j$).
   • $\sum_{j}x_{ij} \leq S_{i}$ ensures that we don’t order more parts than a supplier can provide. This constraint ensures Porsche respects the supplier’s production limits.
3. $x_{ij} \leq M \cdot y_{i} \quad \forall i,j$
   • $x_{ij}$ : is the number of parts ordered from supplier $i$ for factory $j$
   • $y_{i}$ : is a binary variable (0 or 1) that represents whether Porsche chooses to use supplier $i$ or not.
   • $M$ : is a large number that ensures if $y_{i} = 0$, then $x_{ij}$ is forced to be 0 (i.e., no parts can be ordered from that supplier)
   • This constraint guarantees that Porsche can only order parts from a supplier if they have chosen to work with that supplier.
4. $y_{i} \in \{0,1\} \quad \forall i$
   • This ensures that the variable $y_{i}$ is either 0 or 1. In other words, a supplier is either selected (1) or not selected (0).
5. $x_{ij} \geq 0 \quad \forall i,j$
   • $x_{ij}$ : the number of parts ordered, must be a non-negative number. You can’t order a negative number of parts, so this ensures that all orders are positive or zero.

In short, Porsche is trying to make the best decisions in their supply chain, ensuring they get enough parts to keep production going, while minimizing costs and avoiding penalties from delayed parts. This model helps them manage challenges “mathematically.”

Assumptions:

• $c_{ij} = 1500\quad$ (cost of parts and transportation from supplier $i$ to factory $j$)
• $p_{i} = 300\quad$ (penalty for late deliveries)
• $S_{i} = 5000\quad$ (each supplier can supply a maximum of 5000 units)
• $d_{j} = 7000\quad$ (7,000 units of critical parts are needed per factory per year to meet the BEV production goals)
• $M = 1000\quad$ (used to link whether a supplier is selected or not)
• For simplicity, we also assume two factories and three suppliers.

Result:

Solving the mathematical model gives us the following result:

1. The total cost for the optimized solution is 21,000,900EUR. This is the minimum cost to meet the demands of both factories while considering the costs of ordering parts, transportation, and any penalties for delays.
2. All three suppliers are needed to meet the demands of the factories in the most cost-effective way.
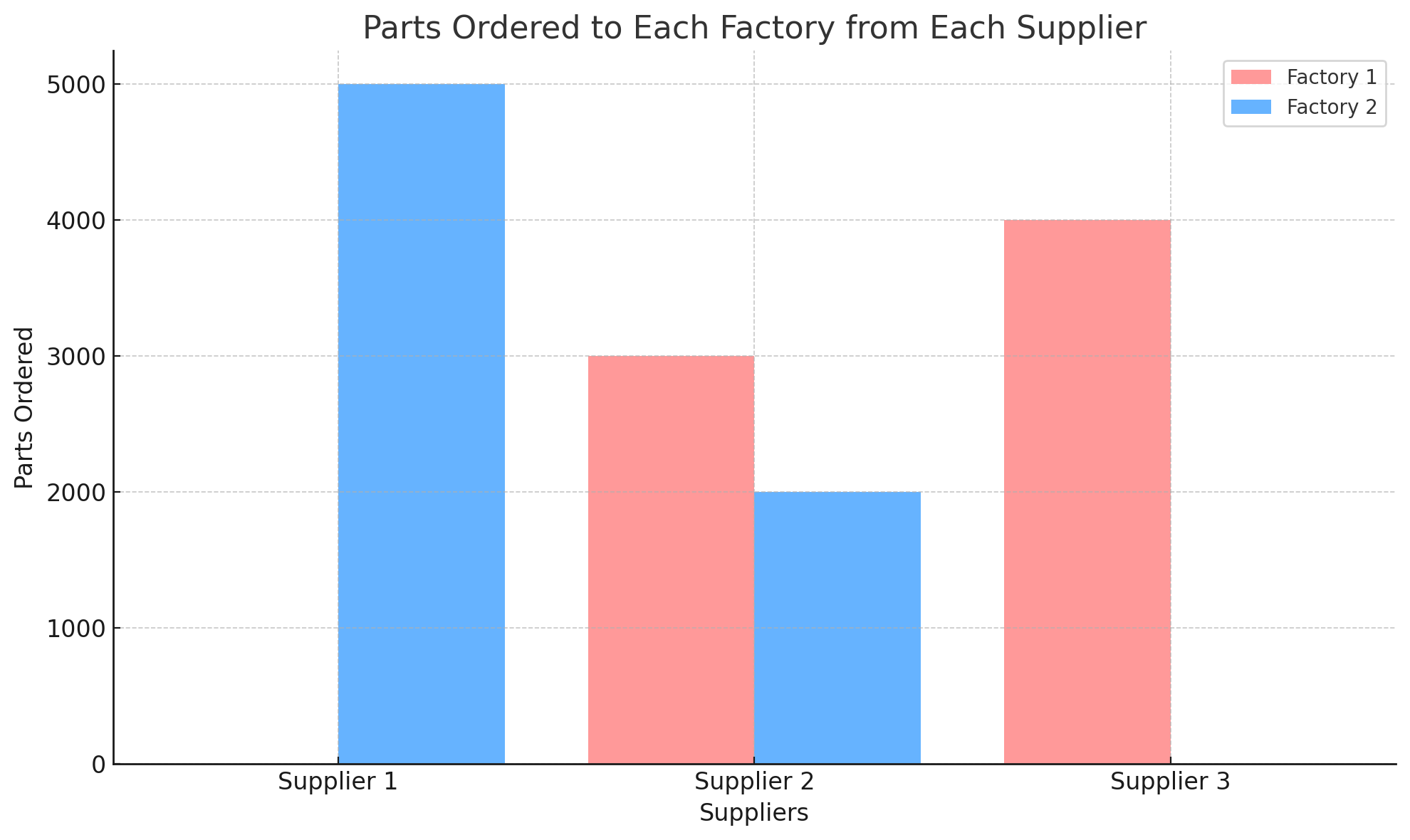
3. Parts ordered from suppliers to factories:
   • Supplier 1: 5000 parts are sent to Factory 2 and reaches its maximum capacity by only supplying Factory 2.
   • Supplier 2: 3000 and 2000 parts are sent to Factory 1 and 2 respectively. Hence, Supplier 2’s capacity is fully utilized across both factories.
   • Supplier 3: 4000 parts are sent to Factory 1. No parts are sent to Factory 2. Supplier 3’s capacity is fully used to meet Factory 1’s demand.

Therefore, Factory 1 receives:

• 3000 parts from Supplier 2
• 4000 parts from Supplier 3
• Total: 7000 parts

and Factory 2 receives:

• 5000 parts from Supplier 1
• 2000 parts from Supplier 2
• Total: 7000 parts

This distribution reflects the constraints of supplier capacities and the goal of minimizing costs, such as transportation and penalties. Following is the visual result: